Transformatörden Yük Çekimi
Transformatörden yük çekimi, sekonder sagılardan bir voltaj çıkışı sağlamak için yapılan mutlak bir olaydır.
Önceki transformatör eğitimlerinde, transformatörün ideal olduğunu, yani transformatör sargılarında çekirdek kayıplarının veya bakır kayıplarının olmadığını varsaymıştık. Bununla birlikte, gerçek dünya transformatörlerinde, transformatör “yüke” konduğundan, transformatörlerin yüklenmesiyle ilgili kayıplar her zaman olacaktır.
İlk önce, bu “yüksüz” durumda, yani sekonder sargısına hiçbir elektrik yükü bağlı olmadığında ve dolayısıyla sekonder akım akmadığı zaman bir transformatöre ne olduğuna bakalım.
Bir transformatörün sekonder taraf sargısı açık devre olduğunda, başka bir deyişle hiçbir şey bağlı olmadığında ve transformatör yükü sıfır olduğunda “yüksüz” olduğu söylenir. Bir transformatörün birincil sargısına bir AC sinüzoidal besleme bağlandığında, birincil besleme voltajının varlığından dolayı birincil bobin sargısından küçük bir IOPEN akımı akacaktır.
İkincil devre açıkken, hiçbir şey bağlı değilken, birincil sargı direnciyle birlikte bir arka EMF, bu birincil akımın akışını sınırlamak için hareket eder. Açıktır ki, bu yüksüz birincil akım ( Io ), gerekli geri emk’yi üretmek için yeterli manyetik alanı sürdürmek için yeterli olmalıdır.
Transformatörün “Yüksüz” Açık Devre Durumu

Yukarıdaki ampermetre, ikincil devre açık devre olmasına rağmen, birincil sargıdan akan küçük bir akımı gösterecektir. Bu yüksüz birincil akım aşağıdaki iki bileşenden oluşur:
- Çekirdek kayıplarını (girdap akımı ve histerezis) besleyen bir faz içi akım, I E.
- Küçük bir akım, manyetik akıyı oluşturan gerilime 90 o’da I M.
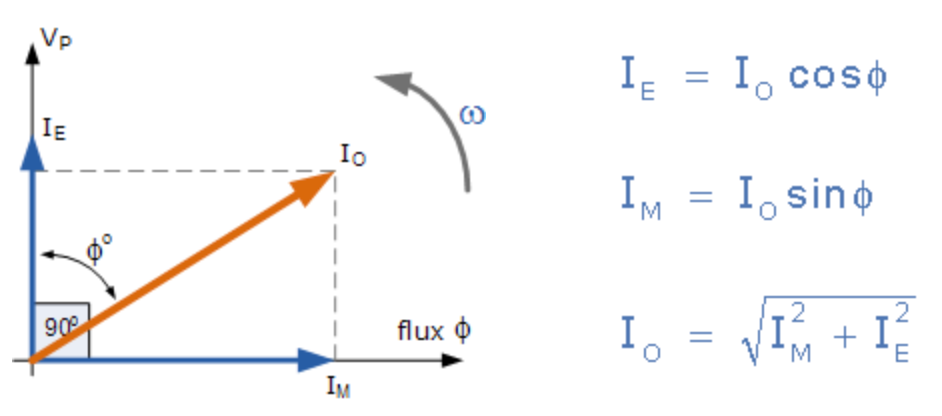
Bu yüksüz birincil akımın, Io’nun transformatörlerin normal tam yük akımına kıyasla çok küçük olduğuna dikkat edin. Ayrıca çekirdekte bulunan demir kayıplarının yanı sıra birincil sargıdaki az miktarda bakır kayıpları nedeniyle, Io besleme voltajının gerisinde kalmaz, Vp tam olarak 90 o , ( cosφ = 0 ), bazı küçük miktarlar olacaktır (faz açısı farkı).
Transformatör “Yükü”
Bir transformatörün sekonder sargısına bir elektrik yükü bağlandığında ve bu nedenle transformatör yükü sıfırdan büyük olduğunda, ikincil sargıda ve yüke bir akım akar. Bu ikincil akım, birincil akımdan çekirdekte oluşturulan manyetik akı tarafından kurulan endüklenen ikincil voltajdan kaynaklanır.
Yükün özellikleri tarafından belirlenen ikincil akım, I S , ana birincil alanın tam tersi yönde akan transformatör çekirdeğinde Φ S , kendinden indüklenen bir ikincil manyetik alan oluşturur , Φ P . Bu iki manyetik alan, ikincil devre açık devre yapıldığında tek başına birincil sargı tarafından üretilen tek alandan daha az manyetik kuvvete sahip birleşik bir manyetik alanla sonuçlanarak birbirine zıttır.
Bu birleşik manyetik alan, birincil akımın, IP‘nin hafifçe artmasına neden olan birincil sargının arka EMF’sini azaltır. Birincil akım, çekirdek manyetik alanı orijinal gücüne geri dönene kadar artmaya devam eder ve bir transformatörün doğru çalışması için birincil ve ikincil manyetik alanlar arasında her zaman dengeli bir koşul bulunmalıdır. Bu, gücün dengelenmesine ve hem birincil hem de ikincil taraflarda aynı olmasına neden olur.

Bir transformatörün dönüş oranının, her bir sargıdaki toplam indüklenen voltajın, o sargıdaki dönüş sayısıyla orantılı olduğunu ve ayrıca bir transformatörün güç çıkışının ve güç girişinin volt çarpı amper’e eşit olduğunu belirttiğini biliyoruz, ( V xI ). Öyleyse:
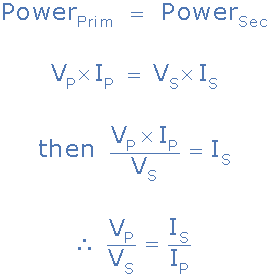
Ancak daha önce, bir transformatörün voltaj oranının, bir transformatörün dönüş oranına eşit olduğunu da biliyoruz: “gerilim oranı = dönüş oranı”. Daha sonra bir transformatördeki voltaj, akım ve dönüş sayısı arasındaki ilişki birbirine bağlanabilir ve bu nedenle şu şekilde verilir:
Trafo Oranı

- Burada:
- N P /N S = V P /V S – gerilim oranını temsil eder
- N P /N S = I S /I P – mevcut oranı temsil eder
Akımın hem voltaj hem de dönüş sayısı ile ters orantılı olduğuna dikkat edin. Bu, sekonder sargıda bir transformatör yüklemesi ile, transformatör sargıları boyunca dengeli bir güç seviyesini korumak için, voltaj yükseltilirse akımın düşürülmesi ve bunun tersi anlamına gelir. Başka bir deyişle, “yüksek voltaj – daha düşük akım” veya “düşük voltaj – daha yüksek akım”.
Bir transformatör oranı, birincil ve ikincil sargıların sayısı, her sargıdaki voltaj ve sargılardan geçen akım arasındaki ilişkiler olduğundan, bilinmeyen herhangi bir voltajın değerini bulmak için yukarıdaki transformatör oran denklemini yeniden düzenleyebiliriz, ( V ) akım, ( I ) veya dönüş sayısı, ( N ) gösterildiği gibi.

Primer sargı tarafından beslemeden çekilen toplam akım , sekonder trafo yüklemesinin bir sonucu olarak yüksüz akım, Io ve ek besleme akımının vektör toplamıdır , I 1 ve besleme voltajının bir açı ile gerisindedir. Φ . Bu ilişkiyi bir fazör diyagramı olarak gösterebiliriz.
Trafo Yükleme Akımı
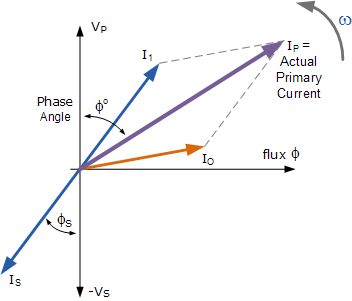
I S ve Io akımları verilirse , birincil akımı I P aşağıdaki yöntemlerle hesaplayabiliriz .
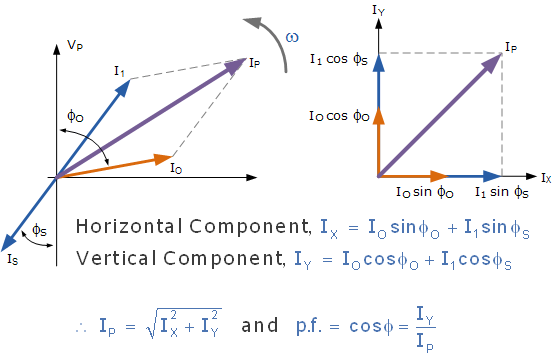
Trafo Yükleme Soru Örneği 1
Tek fazlı bir transformatörün birincil sargısında 1000 dönüş ve ikincil sargısında 200 dönüş vardır. Transformatörlerin beslemeden alınan “yüksüz” akımı, 0,2 gecikmeli güç faktöründe 3 Amper’dir. Birincil bobin akımı Ip, ve karşılık gelen güç faktörünü, ikincil akımı 0,8 endüktifi 280 Amper olduğunda hesaplayın.


Birincil akımın faz açısının, φ P‘nin , ikincil akımın faz açısının, φ S ile hemen hemen aynı olduğunu fark etmiş olabilirsiniz . Bunun nedeni, 3 amperlik yüksüz akımın, beslemeden birincil sargı tarafından çekilen daha büyük 56 amper ile karşılaştırıldığında çok küçük olmasıdır.
Transformatör sargılarının hem empedanslara sahip X- L ve R Fazör diyagramları çizilirken bu empedanslar dikkate alınmalıdır, çünkü bu iç empedanslar transformatör sargılarında gerilim düşüşlerine neden olur. İç empedanslar, sargıların direncinden ve kaçak akıdan kaynaklanan kaçak reaktans adı verilen bir endüktans düşüşünden kaynaklanır. Bu iç empedanslar şu şekilde verilir:
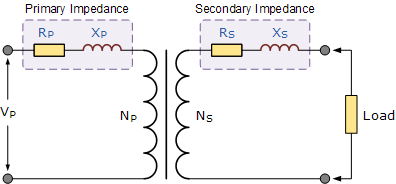
Bu nedenle, bir transformatörün birincil ve ikincil sargıları hem dirence hem de reaktansa sahiptir. Bazen, tüm bu empedans değerlerinin trafonun aynı tarafında bir araya getirilmesi, matematik hesaplamalarını biraz daha kolay hale getirmek için daha uygun olabilir.
Birincil empedansları ikincil tarafa veya ikincil empedansları birincil tarafa taşımak mümkündür. R ve L empedanslarının birleşik değerlerine “Referans Empedanslar” veya “Yansıyan Değerler” denir. Buradaki amaç, transformatör içindeki empedansları birlikte gruplandırmak ve gösterildiği gibi hesaplamalarımızda birincil veya ikincil tarafa yalnızca bir R ve XL referans değer değerine sahip olmaktır.
Trafo Empedanslarını Birleştirme

Transformatörün bir tarafından diğerine bir direnç veya reaktans belirtmek için, dönüş oranının karesi ile çarpmalı veya bölmeliyiz ( Dönüş Oranı 2 ). Bu nedenle, transformatörün ikincil tarafından birincil tarafına empedansları (direnç ve reaktans) atıfta bulunarak (veya yansıtarak), dönüş oranı karesi, N 2 ile çarparız ve birincil empedansları ikincil tarafa atıfta bulunurken, bölmemiz gerekir. oranın karesini döndürür. İkinci yansıma birincil N ile belirlenen bir miktarda R ve X azaltır birinci yansıma Böylece ikincil burada R ve X, arttırır . Empedansların bu referansı veya yansıması, bağlı yük direnci ve reaktans için de aynı şekilde geçerlidir.
Örneğin, 8:1 dönüş oranına sahip birincil tarafa 2Ω’luk bir ikincil direnç belirtmek, yeni bir birincil direnç değeriyle sonuçlanacaktır: 2 x 8 2 = 128Ω , birincil direnç ise 2Ω ile sonuçlanacaktır. ikincil direnç değeri: 0.03125Ω .
Trafo Gerilim Regülasyonu
Bir transformatörün voltaj regülasyonu, transformatör yükü maksimum olduğunda, yani birincil besleme voltajı sabit tutulurken tam yük uygulandığında sekonder terminal voltajındaki değişiklik olarak tanımlanır. Regülasyon, transformatör yüklemesinin yüksek olması sonucunda yük voltajı çok düştüğü için transformatör içinde meydana gelen voltaj düşüşünü (veya artışını) belirler ve bu nedenle performansını ve verimliliğini etkiler.
Voltaj regülasyonu, yüksüz voltajın yüzdesi (veya birim başına) olarak ifade edilir. Daha sonra, E yüksüz ikincil gerilimi ve V tam yüklü ikincil gerilimi temsil ediyorsa , bir transformatörün yüzde düzenlemesi şu şekilde verilir:

Örneğin, bir transformatör yüksüz durumda 100 volt verir ve tam yükte voltaj 95 volta düşerse regülasyon %5 olur. E – V değeri , direncini, R’yi ve daha da önemlisi AC reaktansını X , akımı ve faz açısını içeren sargının iç empedansına bağlı olacaktır.
Ayrıca, yükün güç faktörü daha gecikmeli (endüktif) hale geldikçe voltaj regülasyonu da genellikle artar. Transformatör yüklemesine ilişkin voltaj regülasyonu, değer olarak pozitif veya negatif olabilir, yani referans olarak yüksüz voltaj ile, yük uygulandıkça regülasyondaki değişiklik veya referans olarak tam yük ile değişiklik ve değişiklik olabilir. yük azaltıldığında veya kaldırıldığında regülasyonda yükselir.
Genel olarak, transformatör yükü yüksek olduğunda çekirdek tipi transformatörün regülasyonu, kabuk tipi transformatör kadar iyi değildir. Bunun nedeni, bobin sargılarının birbirine geçmesi nedeniyle kabuk tipi transformatörün daha iyi akı dağılımına sahip olmasıdır.
Transformatörlerle ilgili bir sonraki derste, birden fazla birincil sargısı veya birden fazla ikincil sargısı olan Çoklu Sargılı Transformatöre bakacağız ve daha fazla voltaj veya daha fazla akım sağlamak için iki veya daha fazla sekonder sargıyı nasıl birbirine bağlayabileceğimizi göreceğiz.





